Aby móc przeanalizować sposób, w jaki procesory wykonują podstawowe obliczenia matematyczne, należy zapoznać się z prostymi układami liczącymi. Zaliczymy do nich m. in. sumator.

Sumator

Układ kombinacyjny, który wykonuje dodawanie dwóch (lub więcej) liczb.

Układ kombinacyjny

Układ, w którym stan wyjść zależy jedynie od stanu wejść.

Dodawanie dwóch bitów

Rozważmy dodawanie dwóch liczb 1-bitowych, a i b.

• 0 + 0 = 0
• 0 + 1 = 1
• 1 + 0 = 1
• 1 + 1 = 10

Widzimy, że wynik może być 1- lub 2-bitowy, w zależności od tego, jakie wartości dodajemy. Jest to ważna własność do zapamiętania.

Wynik dodawania dwóch liczb n-bitowych ma n+1 bitów.

Zastanówmy się jednak, czym są poszczególne cyfry w dodawaniu. Wiemy z matematyki, że wynikiem dodawania dwóch składników jest suma. Ale w przypadku, gdy przy dodawaniu wychodzi liczba (czyli co najmniej 2 cyfry), musimy wykonać przeniesienie. Zatem ostatnią sumę możemy zapisać jako

• 1 + 1 = 0 i 1 dalej.

Uzupełnijmy teraz wszystkie powyższe warianty dodawania o wartości przeniesień. Oznaczmy przeniesienie jako c (od ang. carry), a sumę jako s (od ang. sum)

wejścia		wyjścia
a	b	c	s
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

Zatem widzimy, że bit sumy ma wartość 1, gdy jedno z wyjść ma wartość 1, ale nie oba jednocześnie, zaś bit przeniesienia ma wartość 1, gdy oba wejścia mają wartość 1. Zachowanie to jest zgodne z zachowaniem bramek logicznych XOR oraz AND, odpowiednio.

Możemy zatem zapisać to zachowanie jako następujące funkcje logiczne.

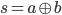
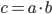
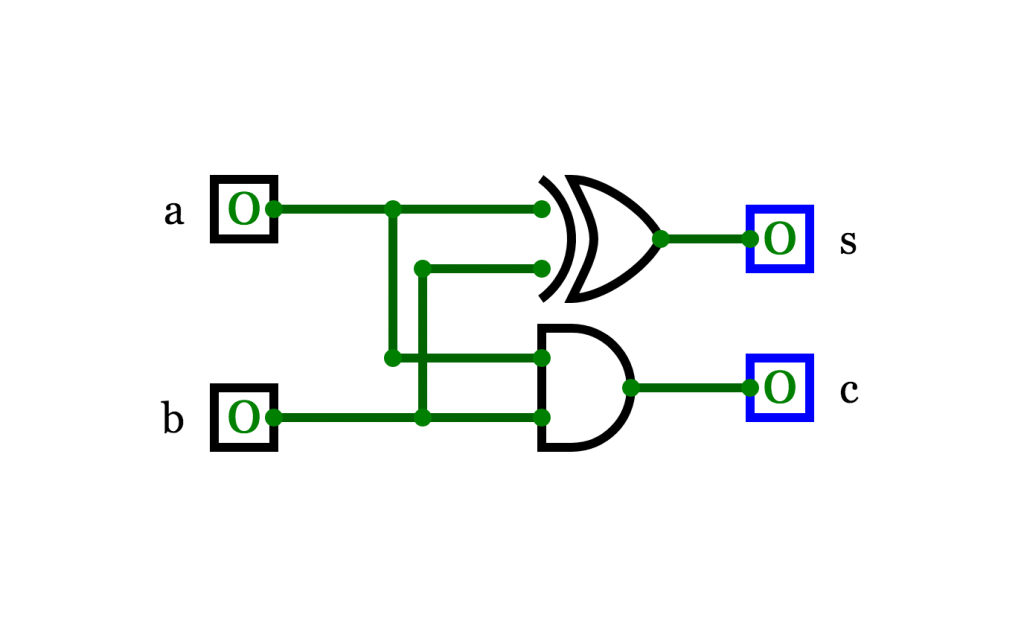
Powyższy układ nazywamy półsumatorem.

Półsumator

Układ kombinacyjny dodający dwa bity – a i b – i produkujący bit s sumy oraz bit c przeniesienia.

Uwzględnienie przeniesienia

Półsumator nie uwzględnia przeniesienia z poprzedniej pozycji, dlatego należy rozważyć układ, który umożliwia dodanie trzeciego bitu.

Oznaczmy przez c_in przeniesienie wejściowe (przeniesienie z poprzedniej pozycji) oraz przez c_out generowane przeniesienie (to, które powstanie w wyniku dodawania).

wejścia			wyjścia
a	b	cin	cout	s
0	0	0	0	0
0	1	0	0	1
1	0	0	0	1
1	1	0	1	0
0	0	1	0	1
0	1	1	1	0
1	0	1	1	0
1	1	1	1	1

Bit przeniesienia

Aby teraz ustalić funkcję logiczną sumy i przeniesienia, trzeba rozważyć trzy wartości wejścia i możliwości, dla których bity te przyjmują wartość 1.

a	b	cin	cout
0	0	0	0
0	1	0	0
1	0	0	0
1	1	0	1
0	0	1	0
0	1	1	1
1	0	1	1
1	1	1	1

Możemy zatem dojść do wniosku, że c_out przyjmuje wartość 1, gdy:

• c_in ma wartość 1 oraz jedno z wejść a i b ma wartość 1, lub gdy
• wejścia a i b mają wartość 1 (niezależnie od wejścia c_in).

Zatem funkcja logiczna opisująca to wyjście przyjmie postać:

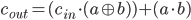
Bit sumy

Ponownie, aby ustalić funkcję logiczną opisującą bit sumy, musimy przeanalizować wartości, dla których funkcja ta przyjmuje wartość 1.

a	b	cin	s
0	0	0	0
0	1	0	1
1	0	0	1
1	1	0	0
0	0	1	1
0	1	1	0
1	0	1	0
1	1	1	1

Tutaj możemy próbować znaleźć pewne wspólne cechy, jak np. to, że gdy c_in=0 oraz a xor b = 1, to s = 1, jednak można zauważyć, że s przyjmuje wartość 1, gdy na wejściu ma nieparzystą liczbę „jedynek”. Takie zachowanie ma bramka XOR, zatem możemy ustalić następujący wzór funkcji logicznej:

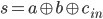
Przygotowanie układu

Podsumowując, otrzymujemy następujące funkcje logiczne opisujące wyjścia budowanego sumatora.

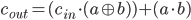
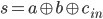
Zwróćmy uwagę, że oba te wzory mają wspólny fragment 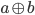– dzięki temu będziemy mogli użyć wyjścia takiej bramki w dwóch miejscach.

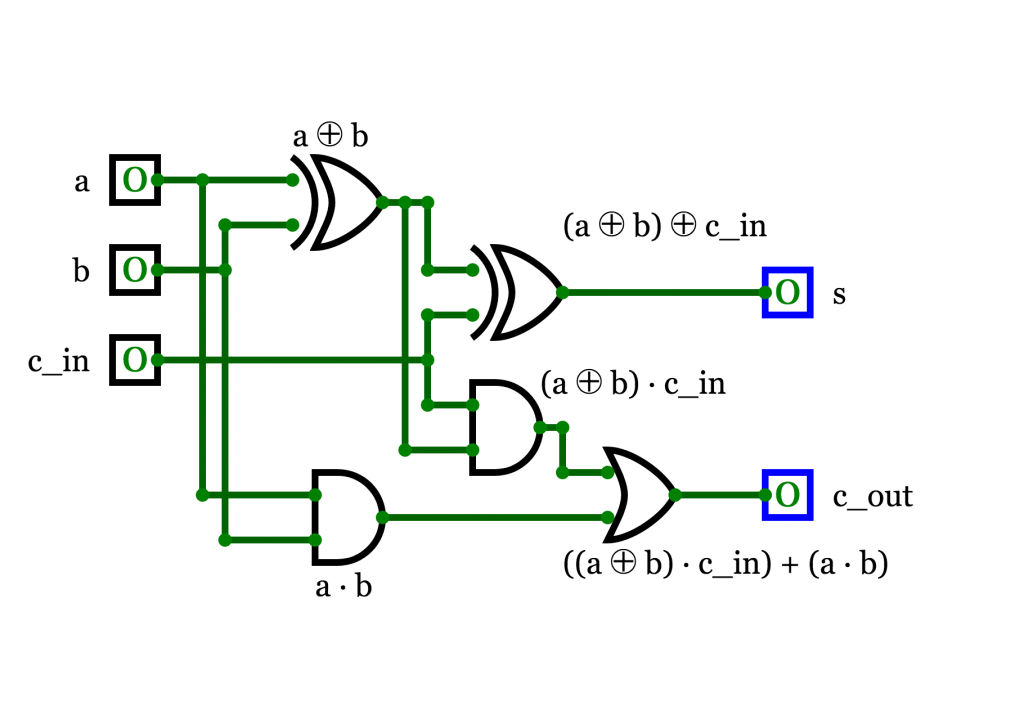
Tak powstały układ nazywamy sumatorem pełnym.

Sumator pełny

Układ kombinacyjny dodający dwa bity – a i b – z uwzględnieniem bitu c_in przeniesienia, produkujący bit s sumy oraz bit c_out przeniesienia.

Uproszczenia notacji

Aby ułatwić notację powyższych układów (i nie powtarzać wciąż wszystkich bramek logicznych), wprowadza się symbole zastępcze zbudowanych układów.