Algebra boolowska została stworzona przez George'a Boole'a w pracach Matematyczna analiza logiki (1847) oraz Rozważania nad prawami myśli (1854). Stała się podstawą rozwoju elektroniki cyfrowej i jest obecna we wszystkich współczesnych językach programowania. Jest także używana w matematycznej teorii zbiorów czy statystyce.
Wartości
Zwykle w algebrze definiujemy liczby (np. 0, 1, 7, …), jednak w algebrze Boole'a definiuje się jedynie wartości prawdy: prawdę oraz fałsz. Wartości te można reprezentować za pomocą bitów (lub: liczb binarnych), odpowiednio 1 oraz 0. Wartości te nie zachowują się jak liczby całkowite, dlatego należy poznać sposób pracy, liczenia, w tej algebrze.
Podstawowe operacje
Podstawowymi operacjami logiki boolowskiej są: koniunkcja (AND, iloczyn logiczny), alternatywa (OR, suma logiczna) oraz negacja (NOT). Operatory te omówiono poniżej.
Koniunkcja
Koniunkcję reprezentuje się za pomocą znaków 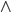 lub
lub  . Jej działanie reprezentuje niniejsza tabela prawdy.
. Jej działanie reprezentuje niniejsza tabela prawdy.
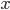 | 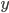 | 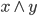 |
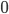 | 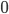 | 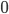 |
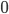 |  | 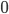 |
 | 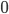 | 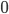 |
 |  |  |
Zauważmy sposób działania iloczynu logicznego:  , gdy
, gdy 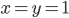 , w przeciwnym wypadku —
, w przeciwnym wypadku — 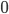 .
.
Alternatywa
Alternatywę reprezentuje się za pomocą znaków 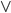 lub
lub 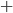 . Jej działanie reprezentuje niniejsza tabela prawdy.
. Jej działanie reprezentuje niniejsza tabela prawdy.
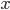 | 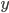 | 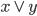 |
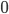 | 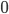 | 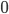 |
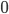 |  |  |
 | 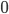 |  |
 |  |  |
Zauważmy sposób działania sumy logicznego: 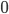 , gdy
, gdy 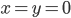 , w przeciwnym wypadku —
, w przeciwnym wypadku —  , czyli prawda, gdy którakolwiek przesłanka jest prawdziwa.
, czyli prawda, gdy którakolwiek przesłanka jest prawdziwa.
Negacja
Negację reprezentuje się za pomocą znaków  lub linią ponad znakiem (
lub linią ponad znakiem (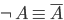 ). Jej działanie reprezentuje niniejsza tabela prawdy.
). Jej działanie reprezentuje niniejsza tabela prawdy.
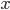 | 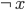 |
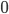 |  |
 | 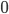 |
Zauważamy sposób działania negacji: zmiana wartości z prawdy na fałsz i odwrotnie.
Prawa algebry logicznej
Jak w każdej algebrze, i w tej określono pewne zasady. Są nimi łączność, rozdzielność, przemienność oraz prawa De Morgana. Pierwsze trzy dotyczą wyłącznie operatorów AND i OR.
Łączność
Łączność jest taką własnością algebry, że kolejność wykonywania działań nie ma znaczenia (uwaga! tylko przy takim samym operatorze).
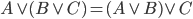
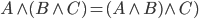
Rozdzielność
Własność rozdzielności pozwala zastosować operator na wartości (operandy) w nawiasach.
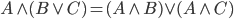
(rozdzielność koniunkcji względem alternatywy
lub
rozdzielność mnożenia względem dodawania)
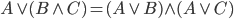
(rozdzielność alternatywy względem koniunkcji
lub
rozdzielność dodawania względem mnożenia, przy czym nie można takiej reguły zastosować w „normalnej” matematyce)
Przemienność
Przemienność oznacza, że kolejność stosowania operatora nie ma znaczenia.
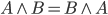
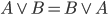
Prawa De Morgana
Dziewiętnastowieczny matematyk, Augustus De Morgan, zaproponował używane do dziś następujące prawa definiujące koniunkcję i alternatywę przy pomocy tych funkcji na wzajem oraz negacji. Przedstawia się je jako następujące „regułki”:
Negacja koniunkcji jest alternatywą negacji.
Negacja alternatywy jest koniunkcją negacji.
Oczywiście możemy zaprezentować także przy ich pomocy same funkcje, a nie ich negacje. Negując obie strony równań, otrzymamy:
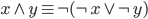
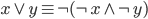
Ważność operatorów
Należy wskazać:
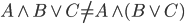
można ułatwić zrozumienie powyższego zapisu, używając następującego:
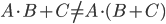
Widzimy teraz analogię do znanej z „codziennej” matematyki kolejności wykonywania działań.
Zasady
Dzięki wprowadzonym wcześniej prawom, możemy przyspieszyć pracę z logiką, stosując następujące własności algebry Boole'a.
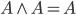 ,
,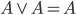 ,
,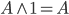 – identyczność koniunkcji — wynik będzie zależeć tylko od A, ponieważ 1 nie wpływa na wynik iloczynu logicznego,
– identyczność koniunkcji — wynik będzie zależeć tylko od A, ponieważ 1 nie wpływa na wynik iloczynu logicznego,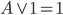 – anihilator alternatywy — coś lub prawda to prawda,
– anihilator alternatywy — coś lub prawda to prawda,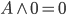 – anihilator koniunkcji — coś oraz fałsz to fałsz,
– anihilator koniunkcji — coś oraz fałsz to fałsz,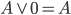 – identyczność alternatywy — coś lub 0 to coś, wynik zależy tylko od A,
– identyczność alternatywy — coś lub 0 to coś, wynik zależy tylko od A,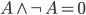 – skoro koniunkcja daje prawdę tylko dla
– skoro koniunkcja daje prawdę tylko dla 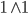 , to nie jest możliwe uzyskanie wyniku innego niż 0 – jeśli A to 1, to negacja 1 da 0, więc otrzymamy
, to nie jest możliwe uzyskanie wyniku innego niż 0 – jeśli A to 1, to negacja 1 da 0, więc otrzymamy 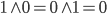 ,
,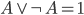 – skoro alternatywa daje prawdę, gdy co najmniej jeden operand (term) jest prawdziwy, to zawsze otrzymamy
– skoro alternatywa daje prawdę, gdy co najmniej jeden operand (term) jest prawdziwy, to zawsze otrzymamy 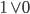 lub
lub 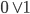 ,
,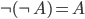 – podwójna negacja „znosi się”,
– podwójna negacja „znosi się”,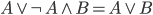 ,
,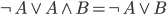 ,
,
Źródła
Boolean Algebra. Wikibooks, open books for an open world. https://en.wikibooks.org/wiki/Electronics/Boolean_Algebra
Boolean Algebra. Wikipedia. https://en.wikipedia.org/wiki/Boolean_algebra
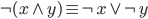
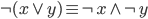
Pingback: Myśląc o Pythonie: Boolean i operatory logiczne - DotPy